문제 링크
12003번: Diamond Collector (Silver)
The first line of the input file contains \(N\) and \(K\) (\(0 \leq K \leq 1,000,000,000\)). The next \(N\) lines each contain an integer giving the size of one of the diamonds. All sizes will be positive and will not exceed \(1,000,000,000\).
www.acmicpc.net
풀이 아이디어
문제 해석을 간단히 하자면, 케이스 안에 다이아몬드를 넣는데
케이스 안에 들어간 다이아몬드들 끼리는 크기 차이가 k 이상 나면 안된다는 문제다.
케이스가 만약 1개라면 '오 투포인터 ㅋ 개꿀 ㅋ' 하면서 문제를 쉽게 풀어 제꼈을 테지만
아쉽게도 이 문제는 케이스가 2개라 약간의 작업을 쳐 놓아야 한다.

우선 투 포인터 알고리즘을 돌리기 위해 sorting을 하고,
Right란 배열을 만들어 각 i번째 인덱스의 투 포인터 결과값을 저장한다.
즉 Right[i]는 case에 i번째 인덱스 보석이 가장 작은 보석으로써 들어갈때, 최대 몇개가 한 케이스 안에 들어갈지를 저장한다.
그림으로 보면 다음처럼 값을 저장한다.
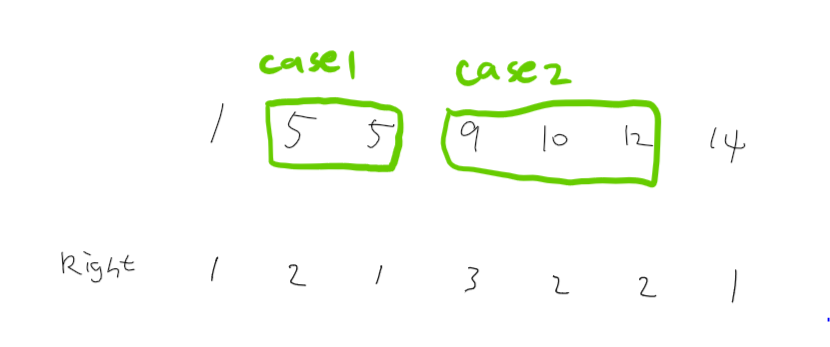
문제에서 요구한 것은 케이스가 2개일 때 이므로,
첫번째로 i번째 인덱스의 값인 Right[i]에
두번째로는 i+Right[i] 번째 인덱스부터 n-1번째 인덱스 중 가장 큰 값을 골라야 한다.
위예시로 들자면, i=1일때 인덱스 값과 1+Right[1] 즉 3일때 인덱스 값인 2와 3의 합이 정답이 된다.
두번째 처럼 특정 값부터 n-1 까지의 Right 값 중 최댓값을 저장해 놓으면 좋은 배열이 필요하다는 생각이 들지 않는가?
본인은 maxRightval이라는 배열을 만들었다.
maxRightval[i] : i이상 중 가장 큰 Right[i] 값 이 되겠다.
이렇게 하면 결국 O(n) 과정만에 계산이 가능하다.
코드는 생각보다 양이 별로 없지만 이러한 과정을 생각해 내는게 좀 쉽지 않는 투 포인터 문제였다고 생각한다.
코드
#include <bits/stdc++.h>
using namespace std;
int main(void){
int n,k;
cin>>n>>k;
int arr[n];
for(int i=0; i<n; i++) cin>>arr[i];
sort(arr,arr+n);
//Right[i] : case에 arr[i]가 가장 작은 다이아로 들어간다 가정했을 때
int Right[n];
int r=0;
for(int l=0;l<n;l++){
while(r<n && arr[r]-arr[l]<=k) r++;
Right[l] = r - l;
}
//maxRightval[i] : i 이상 중 가장 큰 Right[i]의 값
int maxRightval[n+1];
maxRightval[n]=0;
for(int i=n-1; i>=0; i--){
maxRightval[i] = max(maxRightval[i+1],Right[i]);
}
int ans = 0;
for(int i=0; i<n; i++)
ans = max(ans,Right[i]+maxRightval[i+Right[i]]);
cout<<ans;
}'알고리즘 > 백준' 카테고리의 다른 글
| 백준 2638 치즈 - 여러번 bfs를 돌려야하는 문제 (1) | 2021.04.07 |
|---|---|
| 백준 11972 contaminated milk - usaco 브론즈 완전탐색 python 풀이 (0) | 2021.02.07 |
| 백준 2213 트리의 독립집합 - 어떤놈인지까지 찾아야 하는 트리dp c++ (0) | 2021.01.26 |
| 백준 1158 요세푸스 문제 : 큐,벡터로 각각 푸는 2가지 방법 (0) | 2021.01.25 |
| 백준 2150 strongly connected component (0) | 2021.01.24 |